
No dia 20 de março, um conhecido biólogo chamado Atila Iamarino publicou um vídeo que gerou um certo alarme nas pessoas que assistiram por prever que o Brasil teria 1 milhão de mortos por coronavírus em cinco ou seis meses. A estimativa do Atila se baseou no estudo do pesquisador Neil Ferguson (clique aqui para ver o estudo). Este estudo ficou conhecido por ter mudado a postura dos Estados Unidos e do Reino Unido quanto ao enfrentamento da pandemia. Os dois países estavam apostando numa política de não restringir a vida das pessoas e deixar a população ganhar imunidade coletiva.
Essa previsão catastrófica de 1 milhão de mortos deu grande notoriedade ao seu vídeo. Fiquei curioso a respeito e fui pesquisar como a estimativa foi feita. Não quero de nenhuma forma descredenciar o conhecimento do Atila na sua área de especialização. Pesquisei apenas sobre a previsão estatística, que é minha especialidade. Descobri que a estimativa de 1 milhão de mortos é falsa, pois o biólogo inflou sua estimativa com uma série de artifícios duvidosos (para não dizer desonestos).
O estudo do Neil Ferguson estima que se nada fosse feito os Estados Unidos teriam 2,2 milhões e a Grã-Bretanha teriam 510 mil mortes, sem contar os potenciais efeitos negativos da sobrecarga dos sistemas de saúde sobre a mortalidade (“not accounting for the potencial negative effects of health systems being overwhelmed on mortility”).
O biólogo Atila diz em seu vídeo que o estudo do Neil Ferguson indica que esses potenciais efeitos fazem o número de mortos dobrar de valor e fala na possibilidade de mais 4 milhões de mortos nos Estados Unidos e mais de 2 milhões de mortos no Brasil se nada fosse feito. O Neil Ferguson não especula de nenhuma forma quais seriam as dimensões desses efeitos sobre a mortalidade em seu artigo do estudo original. O que reflete uma certa desonestidade intelectual por parte do protagonista do vídeo.
O biólogo brasileiro até poderia indicar que acredita, como sua opinião particular, que as estimativas deveriam ser 10, 15% ou 20% maiores, mas não o dobro. Dizer que as estimativas deveriam ser dobradas sugeriria que os autores do estudo original não foram diligentes e cuidadosos em sua pesquisa. Isso descredenciaria o próprio estudo no qual o Atila se baseou.
Outra observação importante: a pesquisa original foi feita considerando uma letalidade geral dos pacientes baseada na tabela de letalidade por faixa etária dos Estados Unidos e da Grã-Bretanha, que segue abaixo:

Isso faz com que os resultados do estudo não sejam diretamente aplicáveis ao Brasil sem uma adaptação do perfil etário. A população brasileira tem um perfil etário mais jovem que o destes dois territórios, o que faria a letalidade geral ser menor. Veja a diferença entre os perfis etários dos três territórios logo abaixo (Reino Unido e Grã-Bretanha tem população quase coincidentes, dado que a população da Irlanda do Norte é pequena):
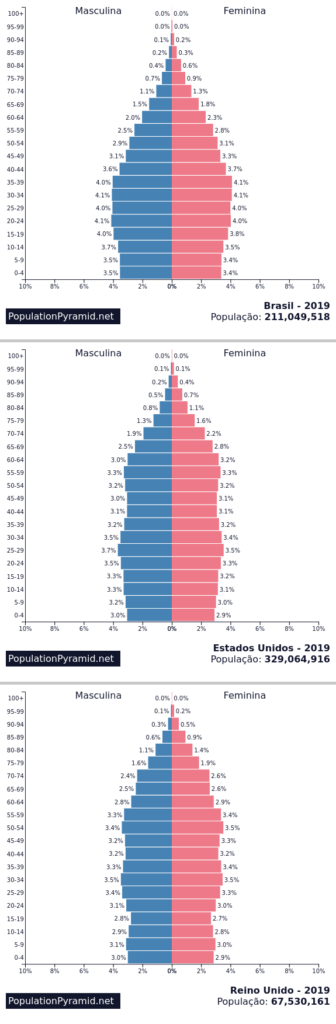
Como pudemos ver acima, o perfil de idade é bem diferente. Seria necessário adaptar as previsões do estudo ao perfil etário brasileiro. A pesquisa do Neil Ferguson também analisa os efeitos das seguintes políticas de intervenção não farmacêutica (sem uso de remédios) que geram uma diminuição da disseminação do vírus (mitigação):
Tabela 2. Políticas de intervenção não farmacêutica (sem uso de remédios) que geram mitigação da disseminação do vírus
| Legenda | Política | Observações |
| CI | Isolamento das pessoas com sintomas em casa por 7 dias | Premissa de que 70% dos domicílios cumpram |
| HQ | Quarentena voluntária de todas as pessoas do domicílio de um paciente com sintomas por 14 dias | Premissa de que 75% dos domicílios cumpram |
| SDO | Distanciamento social dos maiores de 70 anos | Premissa de que 75% dos idosos cumpram |
| SD | Distanciamento social de toda população | Premissa de redução de contatos fora do domicílio em 75% e de aumento de contatos dentro do domicílio em 25% |
| PC | Fechamento de escolas e universidades | Premissa de que 25% das universidades ainda continuem abertas |
A tabela abaixo descreve as previsões de mortos pelo coronavírus para a Grã-Bretanha em diversos cenários das políticas de mitigação descritas acima. Já descartados os cenários onde o governo não faz nada (coluna vermelha), há uma previsão de 120, 71 ou 48 mil mortos nos piores cenários estudados (última linha da tabela).
Tabela 3. O estudo original mostra as estimativas do total de mortos pela doença na Grã-Bretanha ao longo de dois anos em diversos cenários em que as políticas acima são adotadas:
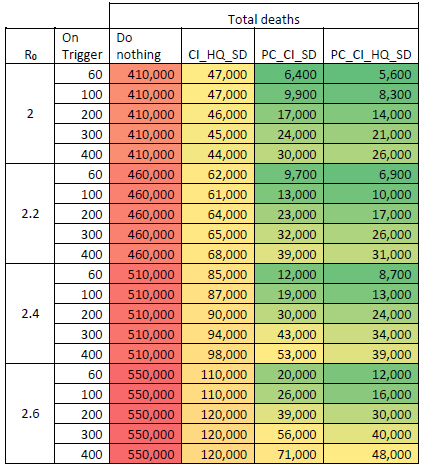
Fiz uma pequena engenharia reversa do que o biólogo brasileiro fez para chegar a sua previsão de 1 milhão de mortos no Brasil. O Brasil tem uma população 3,2 vezes maior que a Grã-Bretanha. O 3,2 foi arredondado para 4 e multiplicado pelo pior cenário mitigado, gerando 4 x 120 mil = 480 mil mortos para o Brasil (lembrando que a tabela acima não se aplica ao Brasil devido as diferenças etárias). Depois, ele arredondou os 480 mil para 500 mil. O biólogo brasileiro dobrou os 500 mil para 1 milhão devido aos potenciais efeitos de sobrecarga do sistema de saúde. Outra possibilidade, fez o cálculo 3,2 x 120 mil x 2 = 768 mil e arredondou este número diretamente para 1 milhão. Lembrando que ele atribuiu a validade de dobrar a quantidade de mortos ao estudo original do Neil Ferguson, porém não há qualquer menção a isso na pesquisa divulgada.
O biólogo arredondou 768 mil para 1 milhão ou arredondou para cima em cascata os valores intermediários até chegar ao valor “desejado”. Usar qualquer um desses procedimentos é inadequado.
Em seu vídeo, o Atila informa que o Brasil está adotando as políticas para evitar a disseminação do vírus (políticas de mitigação), mas usa na sua previsão o cenário mais pessimista possível, desconsiderando que o Brasil já aplicava as políticas que o levariam aos cenários mais otimistas.
Perceba que, na Tabela 3 (acima), sobre as previsões da Grã-Bretanha, o que diferencia a coluna amarela da última coluna verde é o fechamento de escolas e universidades. Essa foi uma das primeiras políticas que o Brasil adotou. Aliás, já adotava todas as políticas que levariam aos cenários da última coluna da Tabela.
Seguindo a lógica do biólogo, ainda usando as estimativas da Grã-Bretanha para prever a situação do Brasil, se você tomar o pior cenário da última coluna da Tabela 3, chegará a uma previsão mais plausível de 3,2 x 48 mil = 153,6 mil mortos. Ajustando o resultado do estudo a pirâmide etária do Brasil, chegaremos a um valor ainda inferior a 153,6 mil.
Este é um número que ainda inspira bastante atenção de nossa parte, mas não chega a 1 milhão. O número de mortos por coronavírus pode até ser maior do que o previsto pela pesquisa do Neil Ferguson, dado que modelos estatísticos são simplificações da realidade e as suas previsões podem errar, mas por essa pesquisa não dá para prever um número maior do que o estimado acima, dado que o Brasil já adotava as políticas de mitigação PC, CI, HQ e SD (Tabela 2).
O fato é que o biólogo estimou um número de mortos pelo menos 6,5 vezes maior do que seria correto baseando-se no estudo do Neil Ferguson e ainda ganhou notoriedade e participação em programas de televisão por isso.
Gostaria de alertar que você tenha cautela e não se desespere ao ver esse tipo de previsão estrambólica sendo divulgada por aí. Ainda que vindas de pessoas que pareçam confiáveis, as previsões podem ser bem erradas e nem sempre passam pela devida checagem nos meios de comunicação de massa.
Achou interessante para um amigo? Compartilhe!
Ficou com alguma dúvida? Deixe nos comentários!
Veja o nosso texto mais recente abordando o coronavírus, a cloroquina e os outros tratamentos!
Quer receber mais artigos como esse, deixe o seu e-mail na barra lateral ou no final da página.

Estatístico e cientista de dados. Apaixonado por aprender e compartilhar conhecimento nas áreas de estatística, economia, finanças e investimentos. Experiência com modelagem estatística e econométrica para a previsão de demanda no transporte rodoviário de passageiros e ferroviário de cargas; análise econômico-financeira de seguros ferroviários; planejamento amostral para pesquisas de campo e construção de modelos de Machine Learning para a análise de propensão de compra, risco de crédito e detecção de fraude.
